
This equation matches the one that we calculated by hand. We can double check our results by inputting our data into the simple linear regression calculator: A one pound increase in weight is associated with a 0.2001 inch increase in height. When weight is zero pounds, the predicted height is 32.783 inches. Sometimes the value for b 0 can be useful to know, but in this example it doesn’t actually make sense to interpret b 0 since a person can’t weigh zero pounds.ī 1 = 0.2001.
Compute simple linear regression equation how to#
Here is how to interpret this estimated linear regression equation: ŷ = 32.783 + 0.2001xī 0 = 32.7830. In our example, it is ŷ = 0.32783 + (0.2001)*x How to Interpret a Simple Linear Regression Equation The estimated linear regression equation is: ŷ = b 0 + b 1*x Step 5: Place b 0 and b 1 in the estimated linear regression equation. Use the following steps to fit a linear regression model to this dataset, using weight as the predictor variable and height as the response variable. Suppose we have the following dataset that shows the weight and height of seven individuals: Example: Simple Linear Regression by Hand which is called the linear regression model. This tutorial explains how to perform simple linear regression by hand. A simple functional form is f(X) 0 + 1X with 0 and 1 being unknown, i.e. Regression Coefficients tell us how much a dependent variable changes with a unit change in the independent variables.Simple linear regression is a statistical method you can use to quantify the relationship between a predictor variable and a response variable.
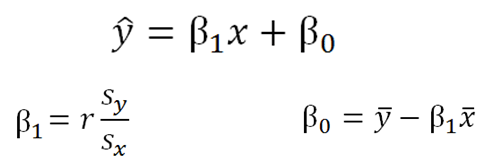
The formula for regression coefficients is given as a = \(\frac\). What is the Formula for Regression Coefficients? Regression coefficients are independent of the change of scale as well as the origin of the plot. What are Regression Coefficients Independent of? They are used in regression equations to estimate the value of the unknown parameters using the known parameters. In statistics, regression coefficients can be defined as multipliers for variables.

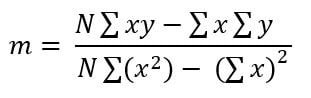


 0 kommentar(er)
0 kommentar(er)
